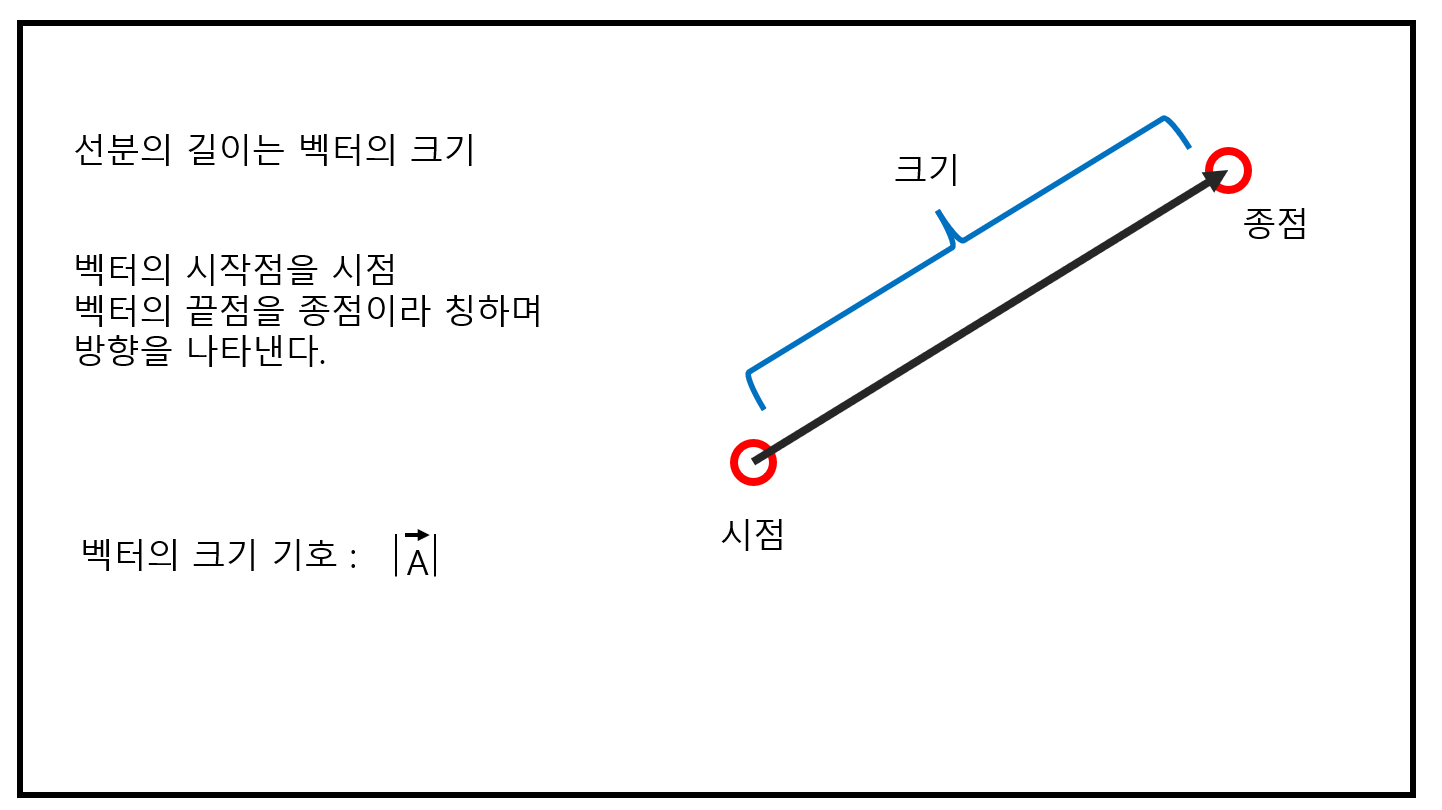
벡터(Vector)란?
크기, 방향을 가진 수학적 대상
두 개의 같은 벡터
크기와 방향이 같으면 같은 벡터라 하고
위치는 상관없다.
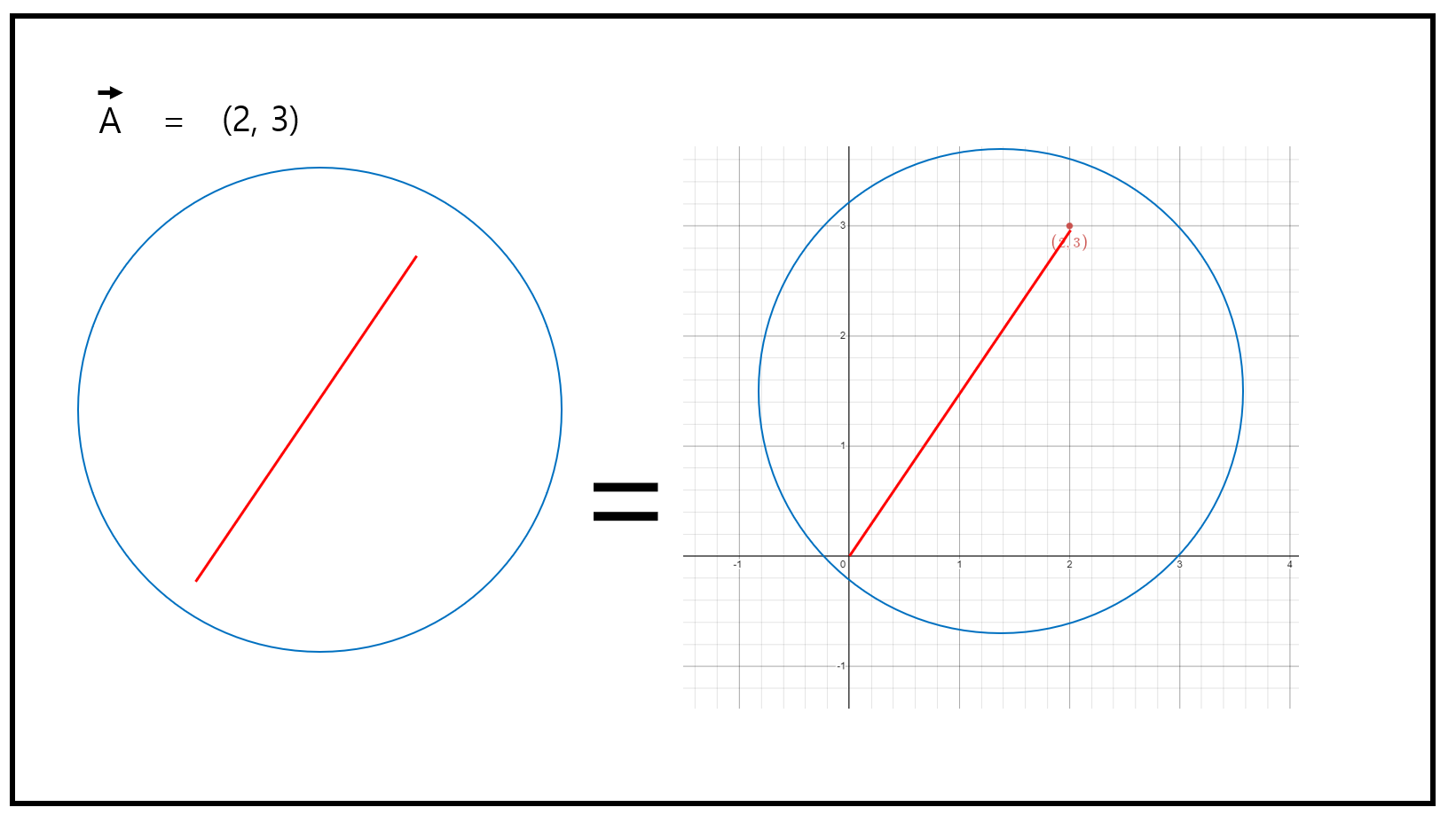
평면 위에 평면 위에 벡터 하나를 두고 좌표 평면 위에 옮기더라도
벡터는 변한 게 없다
즉 벡터를 좌표평면으로 옮겨 (2,3)이라는 것은
원점(0,0)으로부터 (2,3) 종점으로 하는 벡터라고 나타낼 수 있다.

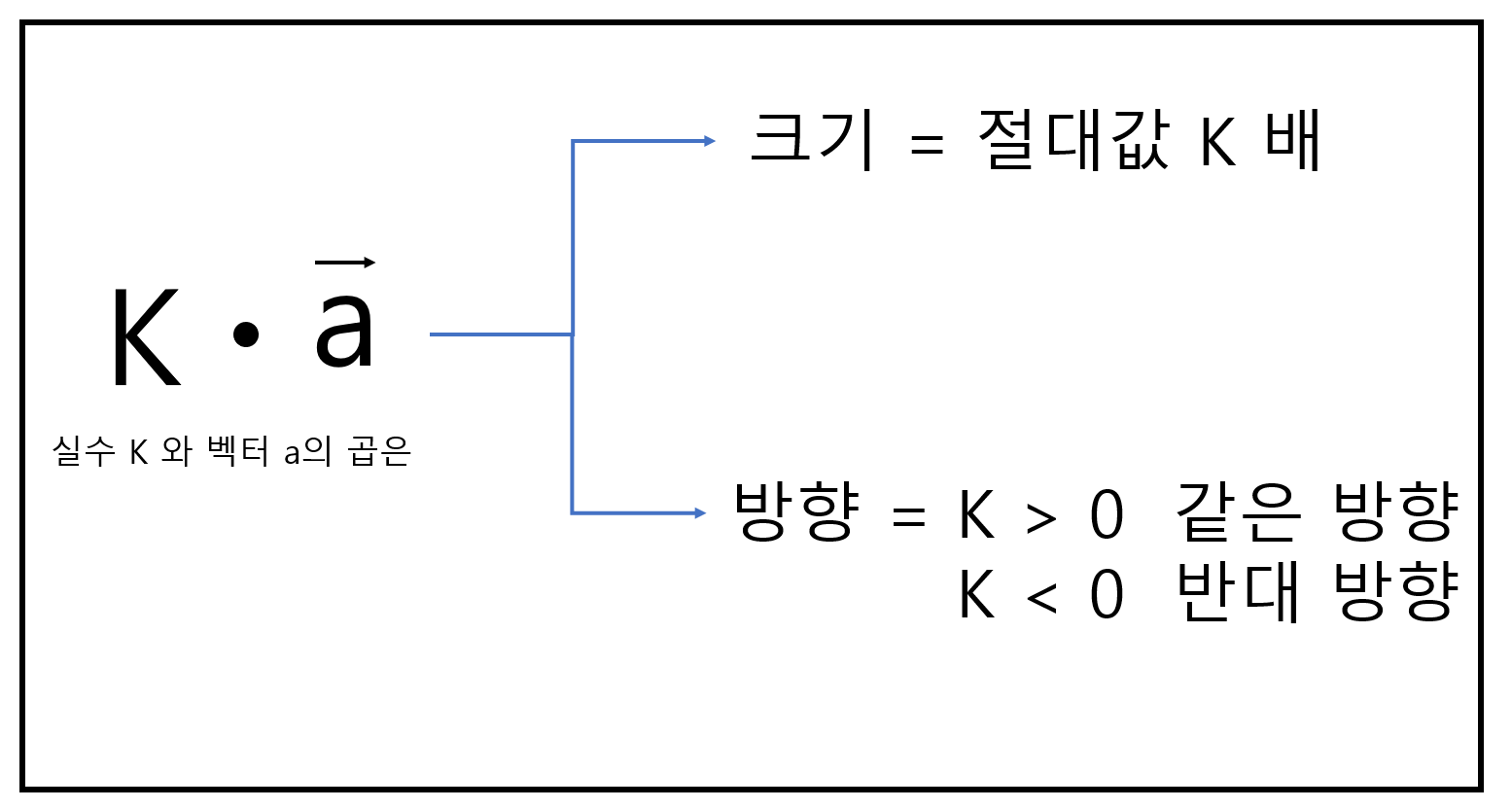
벡터와 실수의 곱
좌표평면 (2,2)에 실수 2를 곱하게 된다면 (4,4)가 나오게 된다.
즉 벡터와 실수의 곱은 벡터의 크기를 n배 늘리겠다는 뜻이며
2가 0보다 크기 때문에 같은 방향으로 2배 늘린다는 뜻이며
만약 -2를 곱하게 된다면 반대방향으로 2배 늘린다는 뜻이 되며
방향이 다르고 크기만 같기 때문에 두 벡터는 같다고 표현하지 않고 평행하다고 말한다.
벡터와 벡터의 덧셈
벡터와 벡터의 덧셈은 한 개의 벡터 종점에서 다른 벡터만큼 움직인 벡터가 된다.

벡터와 벡터의 뻴셈
벡터와 벡터의 뺄셈 역시 덧셈으로 나타낼 수 있는데
똑같이 한 개의 벡터에서 다른 벡터만큼 이동한 벡터가 된다.

선분 A에서 B만큼 움직인 벡터가 되고 이렇게 구한 벡터를 원점으로 그려 본다면 이런 모습이 되는데
이 벡터를 선분 B로 이동시킨다면

평행 사변형 꼴이 된다.

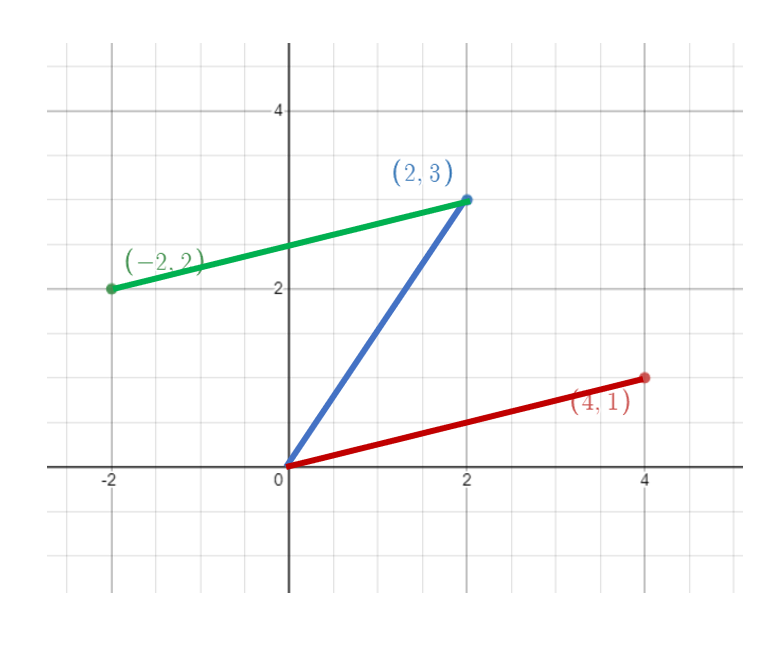
즉 선분 A(2,3) , 선분 B(4,1)을 뺄셈 하게 된다면 점선과 같은 벡터를 얻을 수 있게 된다.
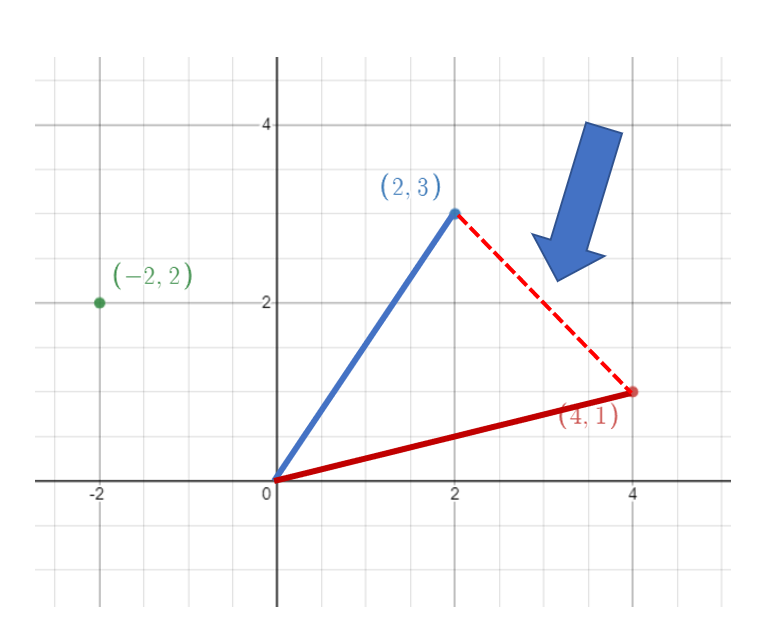
이것을 다르게 말한다면
2차원 평면에서 점 A(2,3)이 있고 점 B(4,1)이 있을 때 두 점을 지나는 벡터 AB의 길이는

점 A에서 점 B를 빼거나 점 B에서 점 A를 뺸 벡터의 크기와 같다
점 A에서 B를 뺸 좌표는 (-2,2)가 되고 원점에서 점 C(-2,2)의 거리는 2 루트 2 가되고
따라서 초록색 벡터의 길이는 2 루트 2가 된다.
벡터의 정규화(Nomalization)
어떤 한 벡터를 벡터의 크기로 나누어서 그 벡터의 크기를 1로 만드는 것이다.
즉 크기가 1이고 방향만 남아있는 벡터를 칭한다.
원점에서 점(10,10)을 지나는 벡터 A가 있다고 할 때
벡터 A를 정규화시키면
먼저 벡터 A의 크기를 구하고 그 값을 각각 x, y에 나눠주면
크기가 1이고 방향 값을 나타내는 벡터가 된다.
벡터의 정규화는 유용하게 사용되는데
만약 플레이어가 보는 방향으로 정규화된 벡터를 알고 있다면
그 벡터의 스칼라곱을 통해 몇 초 뒤에 위치를 예측할 수 있게 된다.

